CUADRADO MÁGICO DE DURERO

El último día hablaba de “aburrimiento”, hoy va de “divertimento”. Así se llama la sección de este blog en la que incluyo ese conglomerado de temas variados que a alguno le parece demasiado simplista y sin categoría para estar en un blog denominado la “Universidad de la Vida”. 

 

Pero “divertimento” no significa sólo lo que normalmente entendemos por divertirse en cuanto a risas, alegrías, jolgorios, etc.; “divertimento” es “diversificación”, alejamiento, divagación, es decir: posibilitar a la mente y a la psique un descanso de concentración de las cosas en las que habitualmente está ocupada. Por eso, quizás, el hablar a veces de cosas intrascendentes es tan productivo y educativo como cualquier otro tema por serio e importante que podamos considerarlo.

Así, que hoy voy a hablar del “Cuadrado mágico de Durero”, que se encuentra en el cuadro “Melancolía I” que ponía en mi artículo sobre elaburrimiento 

 

y en él, observaréis, el famoso “cuadrado mágico” que se encuentra en dicho cuadro. Este cuadrado, de 16 cuadros, tiene una serie de curiosidades que nos van a permitir el divertimento que buscábamos: 

 

Pero antes de entrar en las curiosidades de este “Cuadrado mágico”, ¿por qué Durero lo utilizó en su cuadro?. A 501 años de su realización caben todo tipo de suposiciones, ya que en ninguna parte consta fehacientemente las razones, o explicaciones, del propio autor; pero es una incorporación plenamente coherente con el conjunto del resto de elementos que figuran en el cuadro, como representación de la lucha existencial del pensamiento y sentimiento del hombre ante los misterios y complejidad de las cosas y a la vez su absoluta simpleza cuando se llega a su conocimiento.

 

Estos “cuadrados mágicos” son aparentemente algo sumamente misterioso para quienes no conocen su forma de realización; y en base a dicho misterio se han elaborado cientos de leyendas y profecías desde los tiempos más remotos. Hoy en día están plenamente conocidas y documentadas las diversas técnicas para la elaboración de los mismos en base a fórmulas matemáticas perfectamente definidas, que funcionan en base a lo que se denomina la “constante mágica” de cada cuadrado en virtud del número de cuadros que lo compongan. Así, la “constante mágica” o matemática de un cuadrado de 16 cuadros es 34, como la de 3x3 es 15, o la de 5x5 es 65. Un juego tan popular hoy en día como los sudokus, están realizados con estas técnicas.

Por tanto, es perfectamente factible que la intencionalidad de la inclusión de este cuadrado mágico por Durero en su cuadro Melancolía I tenga como finalidad esa conjunción que siempre se da en nuestras vidas entre la trascendencia, melancolía,  o gravedad de ciertas situaciones y las situaciones y posibilidades inmediatas de ocio, relax o diversión.

Así, que vamos a entrar ya en esa situación de divertimento que nos proporciona este cuadrado en concreto

Para que podamos trabajar mejor con dicho cuadrado, a partir de ahora utilizaré una representación numérica más legible.

La primera curiosidad es la “utilización de la significación ordinal del abecedario”.  Al final de este artículo veremos otras varias referencias a este tema, pero esta primera curiosidad es precisamente la que hace que algunos comentaristas de este cuadrado expliquen por qué Durero utilizó el cuadrado de 4x4 cuya constante es, como dije, 34.

Estos autores dicen que si cogemos las iniciales de “Cuadrado de Durero”, el ordinal alfabético de las mismas es, precisamente 3 y 4

Como he dicho, más adelante veremos otras observaciones al respecto que de alguna forma minimizan o anulan la fortaleza de esta hipótesis.

Bien, a continuación, viene la primera pregunta ¿cuántas veces se cumple esa suma de 34 en el cuadrado de Durero?. Según algunos entendidos en el tema, en un cuadrado mágico de 4x4, con valores de 1 a 16, existen 86 posibilidades distintas de agrupar 4 números que sumen 34. Bien, yo no he sido capaz de lograrlo, pero no lo voy a cuestionar; solo pretendo un rato de divertimento, y que todos los que lean este artículo se queden con una sensación de relax agradable y no “convencidos” de la verdad científica o matemática de un número u otro de posibilidades.

Así que vayamos paso a paso según lo más común

El primer paso de cualquier cuadrado mágico es comprobar su exactitud en la suma de los valores de cada fila, cada columna y las dos diagonales centrales

 Fácilmente se puede comprobar que se da ese resultado de 34 en las 10 líneas

A continuación mostramos otras dos sumas de 34: se trata de las 4 casillas centrales y de las cuatro esquinas. A este efecto, algunos tratadistas lo denominan “efecto explosión” o “expansión”, tratando de expresar que lo que se cumple en un núcleo central unido y poderoso, se expande a los cuatro vientos manteniendo su esencia:

Estas sumas algunos autores las encuadran en las del grupo de “movimientos de ajedrez” que más adelante comentaremos

Llevamos ya 12 sumas de 34

Como otra variante del denominado efecto expansión, algunos analistas de estos cuadrados hablan de la “expansión central”, que es la que se localiza en los cuadrados intermedios entre el núcleo central y las esquinas

Vemos que con dichas cuadrículas se logran 2 nuevas sumas de 34. Alcanzamos, pues, ya las 14

A continuación, tenemos el que se denomina “efecto traslación o multiplicación”, que expresaría la esencia de la fortaleza de la unidad y el ejemplo; es decir: el comportamiento de pequeños grupos se traslada al colectivo o grupo común.

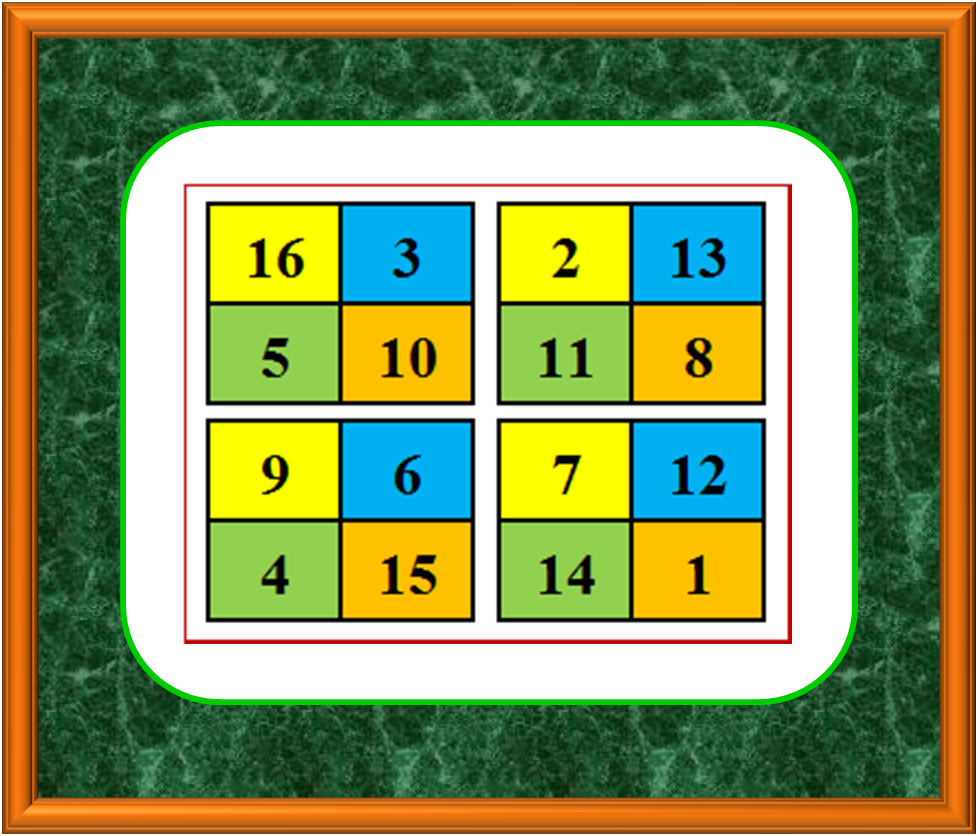
Así que cada pequeño cuadrado también suma 34, con lo que logramos alcanzar la cifra de 18 sumas de 34. Esto va bien.

 

Una variación de esta “multiplicación”, es cuando se entiende que los elementos pueden “afectar” por sí mismos (¡¡pero en pareja!!) fuera de su núcleo natural inicial. Esta parábola o similitud es la que podría aplicarse a cuando (según los evangelios) Jesús mandó a sus discípulos ¡¡de dos en dos!! a que preparasen la pascua y su dispersión por los alrededores “porque ya estaban preparados para la misión que tenían encomendada”

Veamos cómo se traduciría este efecto desde la figura anterior. 

Con lo cual se observan 8 nuevas combinaciones de cuadrículas que vuelven a sumar 34, con lo que ya acumulamos 26

Otra de las variantes constructivas de estos cuadrados desde las que podríamos denominar “perspectivas trascendentes” (teosóficas o metafísicas), es la del “Desplazamiento” (o desplazamiento ordinal) que consistiría en la traslación lateral y vertical de las posiciones a sumar de cada cuadrado 2x2. En nuestro caso, vendría representada por los siguientes grupos de cuadrículas:

En la que se puede observar que los valores a sumar en cada uno de los cuatro casos es de cuadrículas que ocupan las mismas posiciones en cada uno de los cuatro cuadrados pequeños

Bien, y así sumamos otras cuatro opciones de valor 34, por lo que hemos logrado ya 30

Comentamos ya anteriormente que algunos autores encuadraban la generación de las "torres" del cuadrado en la técnica de los “movimiento de ajedrez”, en vez de los efectos de la “explosión” de la fuerza nuclear del cuadrado central; en cualquier caso, podemos observar otras dos relaciones más de movimientos de ajedrez: la del movimiento del caballo, y la del movimiento del alfil. De acuerdo con dichas semejanzas, los emparejamientos de cuadros serían:

Con lo que lograríamos otros cuatro grupos de números que suman 34; es decir, ¡¡ ya tenemos logrados 34 grupos que suman 34!!.

Otras de las figuras más simbólicas desde tiempos inmemoriales son la cruz, como símbolo de fin de la vida, y la cometa, como símbolo de plenitud de vida … aunque como bien puso de relieve un estudioso del tema: “la cometa, por muy divertida que sea su apariencia externa, no podrá volar si no la sostiene una buena cruz en su interior”

OK, pues vamos a ver qué cometas, o cruces encontramos en el cuadrado de Durero.

Pero antes, es imprescindible señalar otra de las habilidades de Durero en todo este divertimento: ¿Os habéis fijado en las dos cuadrículas centrales de la fila inferior?, pues forman el número 1514, año en que pintó el cuadro.

Y hecha esta precisión vamos a ver si encontramos alguna otra suma de 34. 

Veamos la siguiente figura:

Como veis, aquí el juego es un poco diferente: ahora nos movemos con una especie de cruz con cuatro puntos (soporte de cometa). En esta opción se prescinde de las cuatro esquinas del cuadrado, y las cuatro cruces se construyen desplazando las mismas de izquierda a derecha, y volteándolas en vertical, formándose cuatro cruces apoyadas (por los pies o la cabeza) en las dos cuadrículas que forman el año 1514. Y, si comprobamos….¡¡oh cielos, también suman 34 cada una de ellas!!, así que alcanzamos las 38 sumas de valor 34.

Finalmente, una más de las líneas teosóficas que vienen atribuyéndose a la construcción de todos estos cuadrados mágicos es la que se conoce con el nombre de “conservación”  o  “enrocamiento”, y viene a expresar la idea de que siempre hay que conservar el control desde el núcleo central, o de que siempre hay que tener la posibilidad de volver a un punto de origen. Bajo esta perspectiva, las combinaciones a realizar son de dos cuadrículas del núcleo central con otras dos cuadrículas de las esquinas.

En el caso del cuadro que estamos viendo serían las siguientes:

Obsérvese que en esta última figura que presento, bajo esa denominación de “conservación”  o “enrocamiento”, que podría equivaler a la idea de volver al principio, o mantener el principio sea cual sea el camino expansivo antes recorrido, las dos figuran que se forman contienen los siguientes elementos ya vistos con anterioridad:

- en cada una de ellas hay influencia de cada línea y de cada fila, y de cada diagonal

- del núcleo central y de los extremos de la expansión

- figuras de movimiento de alfil y de caballo

- y figuras de cruz de cometa

… es como si hubiésemos cerrado el círculo de nuestras cavilaciones ….tal como representa todo el cuadro de Durero.

Y para finalizar este artículo de divertimento y “cultura de la Universidad de la Vida”, un par de observaciones sobre el cuadro y el autor desde la perspectiva de “ordinalidad” de las letras del alfabeto. Ojo, no confundir la ordinalidad, o posición que ocupan en el alfabeto, con el concepto más técnico y esotérico de “numerología de la letras”. 

Pues bien, voy a mostraros dos curiosidades al respecto de este cuadro denominado  “Melancolía I” del autor  “ALBRECHT DVRER”, tal como él se hacía llamar.

Empecemos aplicando el valor ordinal alfabético al nombre del autor.

Lo primero que vemos es que sus iniciales A y D se corresponden a los guarismos 1 y 4, que coinciden con el primero y el último de la fecha del cuadro (1514)

Si sumamos las posiciones de cada una de las letras de ALBRECHT DVRER tendremos: (1 +12+ 2+ 18+ 5+ 3+8 +20) + (4+ 22 +18 +5+ 18) = 136 … que es  ¡¡precisamente!! el valor suma de las 16 cuadrículas del cuadrado del que venimos hablando

Y ahora pasemos al nombre del cuadro: “MELANCOLÍA I”. Para ello, vamos a transformar el número romano I por sus letras en alemán: Eins; con lo cual el nombre del cuadro sería “Melancolía eins”. Pues bien, las posiciones alfabéticas de ese nombre son: (13 +5 +12 +5+ 14+3 +15+ 12+ 9 +1) + (5 +9 + 14 +19)…¡¡¡que también suman 136!!!

¿Por qué hizo Durero todo esto hace 500 años?;  ¿para qué  lo hizo?; ¿quizás para que nosotros tuviésemos hoy un rato de divertimento gracias a él? Nunca lo sabremos; pero podríamos pensar así y disfrutarlo aún mucho más.

Confío en que más que cansados os sintáis deseos de bucear por internet buscando más cosas semejantes.

Si yo fuera Durero, me encantaría que lo compartieseis con todas vuestras amistades. No siéndolo, me agradaría muchísimo más.

Gracias por todo

-------------------------------------

OBSERVACIÓN : Si alguien quiere este artículo en soporte Word o PDF no tiene más que pedírmelo por email